B_树的B+树

B_树
B-树就是B树。m阶B_树满足或空，或为满足下列性质的m叉树：
树中每个结点最多有m棵子树
根结点在不是叶子时，至少有两棵子树
除根外，所有非终端结点至少有⎡m/2⎤棵子树
有s个子树的非叶结点具有 n = s-1个关键字，结点的信息组织为:(n,A0,K1,A1,K2,A2 … Kn，An)。这里：n为关键字的个数，ki（i=1,2,…,n)为关键字，且满足Ki小于Ki+1,，Ai(i=0,1,..n)为指向子树的指针。
所有的叶子结点都出现在同一层上，不带信息（可认为外部结点或失败结点）。
关键字集合分布在整颗树中
任何一个关键字出现且只出现在一个结点中
搜索有可能在非叶子结点结束
其搜索性能等价于在关键字全集内做一次二分查找
只适用于随机检索，不适用于顺序检索。
有结点的平衡因子都为零
M阶B-树中含有N个关键字，最大深度为log⎡m/2⎤(n+1)/2+2
B_树中结点的插入

m代表B_树的阶，插入总发生在最低层
插入后关键字个数小于等于 m-1,完成。
插入后关键字个数等于m,结点分裂，以中点数据为界一分为二，中点数据放到双亲结点中。这样就有可能使得双亲结点的数据个数为m,引起双亲结点的分裂，最坏情况下一直波及到根，引起根的分裂——B_树长高。
3阶B_树的插入。每个结点最多3棵子树，2个数据；最少2棵子树，1个数据。所以3阶B_树也称为2-3树。

B_树中结点的删除

删除发生在最底层
被删关键字所在结点中的关键字数目大于等于 m/2 ，直接删除。
删除后结点中数据为⎡m/2⎤-2，而相邻的左（右）兄弟中数据大于⎡m/2⎤-1，此时左（右兄弟）中最大（小）的数据上移到双亲中，双亲中接（靠）在它后（前）面的数据移到被删数据的结点中
其左右兄弟结点中数据都是⎡m/2⎤-1，此时和左（右）兄弟合并，合并时连同双亲中相关的关键字。此时，双亲中少了一项，因此又可能引起双亲的合并，最坏一直到根，使B-树降低一层。
删除不在最底层
在大于被删数据中选最小的代替被删数据，问题转换成在最底层的删除
B+树
在实际的文件系统中，用的是B+树或其变形。有关性质与操作类似与B_树。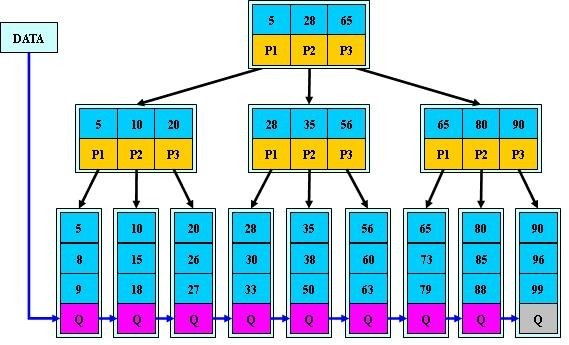

差异：

有n棵子树的结点中有n个关键字，每个关键字不保存数据，只用来索引，所有数据都保存在叶子节点。
所有叶子结点中包含全部关键字信息，及对应记录位置信息及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。(而B树的叶子节点并没有包括全部需要查找的信息)
所有非叶子为索引，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B树的非终节点也包含需要查找的有效信息)
非叶最底层顺序联结，这样可以进行顺序查找
B+特性

所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
不可能在非叶子结点命中
非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层
更适合文件索引系统
B+树插入操作的平均时间复杂度为O(logn)，最坏时间复杂度为O(logn)
查找过程

在 B+ 树上，既可以进行缩小范围的查找，也可以进行顺序查找；
在进行缩小范围的查找时，不管成功与否，都必须查到叶子结点才能结束；
若在结点内查找时，给定值≤Ki， 则应继续在 Ai 所指子树中进行查找
插入和删除的操作：类似于B_树进行，即必要时，也需要进行结点的“分裂”或“合并”。

为什么说B+tree比B树更适合实际应用中操作系统的文件索引和数据库索引？

B+tree的磁盘读写代价更低
B+tree的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B树就比B+树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。
B+tree的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
B树和B+树都是平衡的多叉树。B树和B+树都可用于文件的索引结构。B树和B+树都能有效的支持随机检索。B+树既能索引查找也能顺序查找.